 Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея, рассказал АиФ.ru о делении на ноль:
Евгений Ширяев, преподаватель и руководитель Лаборатории математики Политехнического музея, рассказал АиФ.ru о делении на ноль:
1. Юрисдикция вопроса
Согласитесь, особенную провокационность правилу придает запрет. Как это нельзя? Кто запретил? А как же наши гражданские права?
Ни конституция РФ, ни Уголовный кодекс, ни даже устав вашей школы не возражают против интересующего нас интеллектуального действия. А значит, запрет не имеет юридической силы, и ничто не мешает прямо тут, на страницах АиФ.ru, попробовать что-нибудь разделить на ноль. Например, тысячу.
2. Разделим, как учили
Вспомните, когда вы только узнали, как делить, первые примеры решали спроверкой умножением: результат, умноженный на делитель должен был совпасть сделимым. Не совпал — не решили.
Пример 1. 1000 : 0 =...
Забудем на минуту про запретное правило и сделаем несколько попыток угадать ответ.
Неправильные отсечёт проверка. Перебирайте варианты: 100, 1, −23, 17, 0, 10 000. Для каждого из них проверка даст один и тот же результат:
100 · 0 = 1 · 0 = − 23 · 0 = 17 · 0 = 0 · 0 = 10 000 · 0 = 0
Ноль умножением все превращает в себя и никогда в тысячу. Вывод сформулировать несложно: никакое число не пройдет проверку. Т. е. ни одно число не может быть результатом деления ненулевого числа на ноль. Такое деление не запрещено, а просто не имеет результата.
3. Нюанс
Чуть не упустили одну возможность опровергнуть запрет. Да, мы признаем, что ненулевое число не разделится на 0. Но может быть, сам 0 сможет?
Пример 2. 0 : 0 = ...
Ваши предложения для частного? 100? Пожалуйста: частное 100, умноженное на делитель 0, равно делимому 0.
Еще варианты! 1? Тоже подходит. И −23, и 17, и все-все-все. В этом примере проверка на результат будет положительной для любого числа. И по-честному, решением в этом примере надо называть не число, а множество чисел. Всех. А так недолго договориться и до того, что Алиса это не Алиса, а Мэри-Энн, а обе они — сон кролика.
4. Что там про высшую математику?
Проблема разрешена, нюансы учтены, точки расставлены, все прояснилось — ответом для примера с делением на ноль не может быть ни одно число. Такие задачки решать — дело безнадежное и невозможное. А значит... интересное! Дубль два.
Пример 3. Придумать, как разделить 1000 на 0.
А никак. Зато 1000 можно без трудностей делить на другие числа. Ну, давайте хотя бы делать, что получается, пусть даже изменив поставленную задачу. А там, глядишь, увлечемся, и ответ сам собой объявится. Забываем на минуту про ноль и делим на сто:
1000 : 100 = 10.
Сотня далека от нуля. Сделаем шаг к нему, уменьшив делитель:
1000 : 50 = 20.
Еще один:
1000 : 40 = 25.
И потопали дальше:
1000 : 25 = 40,
1000 : 20 = 50,
1000 : 10 = 100,
1000 : 8 = 125,
1000 : 5 = 200,
1000 : 4 = 250,
1000 : 2 = 500,
1000 : 1 = 1000.
Очевидная динамика: чем ближе делитель к нулю, тем больше частное. Тенденцию можно наблюдать и дальше, переходя к дробям и продолжая уменьшать числитель:
Осталось заметить, что к нулю мы можем подойти как угодно близко, делая частное сколь угодно большим.
В этом процессе нет нуля и нет последнего частного. Мы обозначили движение к ним, заменив число на последовательность, сходящуюся к интересующему нас числу:
При этом подразумевается аналогичная замена и для делимого:
1000 ↔ { 1000, 1000, 1000,... }
Стрелки не зря поставлены двусторонними: некоторые последовательности могут сходиться к числам. Тогда мы можем поставить в соответствие последовательности ее числовой предел.
Посмотрим на последовательность частных:
Она растет неограниченно, не стремясь ни к какому числу и превосходя любое. Математики добавляют к числам символ ∞, чтобы иметь возможность рядом с такой последовательностью поставить двустороннюю стрелку:
Сопоставление числам последовательностей, имеющих предел, позволяет предложить решение к третьему примеру:
При поэлементном делении последовательности, сходящейся к 1000, на последовательность из положительных чисел, сходящуюся к 0, получим последовательность, сходящуюся к ∞.
5. И здесь нюанс с двумя нулями
Что будет результатом деления двух последовательностей положительных чисел, сходящихся к нулю? Если они одинаковые, то тождественная единица. Если к нулю быстрее сходится последовательность-делимое, то в частном последовательность снулевым пределом. А когда элементы делителя убывают гораздо быстрее, чем у делимого, последовательность частного будет сильно расти:
Неопределенная ситуация. И так и называется: неопределенность вида 0/0. Когда математики видят последовательности, подходящие под такую неопределенность, они не бросаются делить два одинаковых числа друг на друга, а разбираются, какая из последовательностей быстрее бежит к нулю и как именно. И в каждом примере будет свой конкретный ответ!
6. В жизни
Закон Ома связывает силу тока, напряжение и сопротивление в цепи. Часто его записывают в такой форме:
Позволим себе пренебречь аккуратным физическим пониманием и формально посмотрим на правую часть как на частное двух чисел. Вообразим, что решаем школьную задачу по электричеству. В условии дано напряжение в вольтах и сопротивление в омах. Вопрос очевиден, решение в одно действие.
А теперь заглянем в определение сверхпроводимости: это свойство некоторых металлов обладать нулевым электрическим сопротивлением.
Ну что, решим задачку для сверхпроводящей цепи? Просто так подставить R = 0 не выйдет, физика подкидывает интересную задачу, за которой, очевидно, стоит научное открытие. И люди, сумевшие поделить на ноль в этой ситуации, получили Нобелевскую премию. Любые запреты полезно уметь обходить!









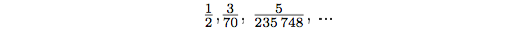
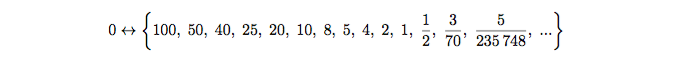

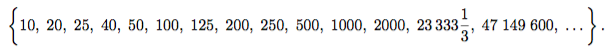


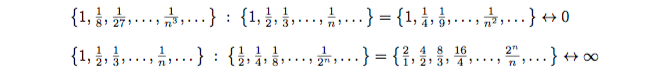
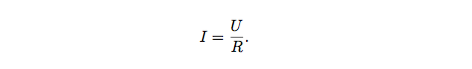

 Математики в России перевелись или их у нас сманили?
Математики в России перевелись или их у нас сманили?  Замученные дети. Учат высшую математику, но не решают элементарных задач
Замученные дети. Учат высшую математику, но не решают элементарных задач  Россия спешит на помощь. Норвежцев учат математике по-русски
Россия спешит на помощь. Норвежцев учат математике по-русски  «Профессор Соня». Почему Софья Ковалевская оказалась не нужна России
«Профессор Соня». Почему Софья Ковалевская оказалась не нужна России 

